CS106B Assignment5

发表于 阅读次数： 本文字数： 1.8k 阅读时长 ≈ 3 分钟

Foreword

记录2022 winter的CS106B Assignment5

Big-O Analysis

分析一下几个函数的时间复杂度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
The big-O time complexity of the function...

... printH is O(n^2),
... printC is O(n),
... printI is O(n^2),
... printP is O(n^2),
... printChip is O(n^2),
... countTriples is O(n^3),
... printCycle_v1 is O(n^2),
... printCycle_v2 is O(n^2),
... printCycle_v3 is O(n),
... recursivePuzzle is O(n),
... recursiveEnigma is O(logn),
... maximumSingleSellProfit_v1 is O(n^2), and
... maximumSingleSellProfit_v2 is O(nlogn)

Matchmaker Revisited

对于上一个Assignment的最大权匹配有个带花树算法(OIWIKI上甚至有)

让估计它的复杂度

估计出来大概是$O(n^3)$，假设我的电脑一秒能有$10^8$的运算量的话

和OIWIKI上写的复杂度也差不多

On Efficiency

讲了一个IBM的故事..告诫学生对于一个算法除了时间复杂度还要考察很多方面..

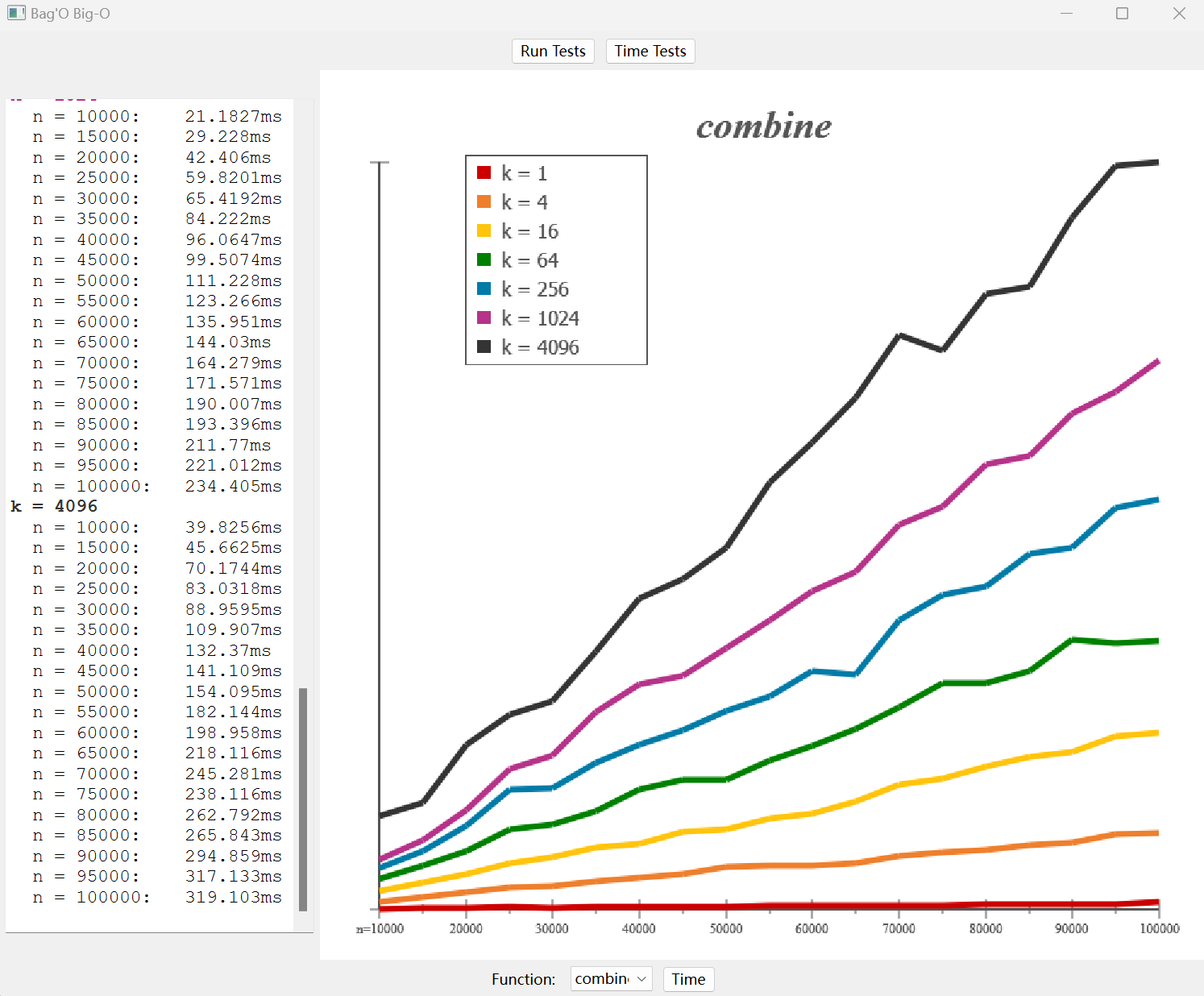
Combine

有$k$个有序的，长短可能不一的数组，怎么把它们有序的合并成一个数组

要求用$O(nlogk)$的算法，思想大概是$k$层递归，每层把当前$k$个数组分成前一半和后一半

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Vector<DataPoint> combineTwoSequences(Vector<DataPoint> s1, Vector<DataPoint> s2) {
    Vector<DataPoint> res;
    int i = 0, j = 0;
    while (i < s1.size() || j < s2.size()) {
        if (i == s1.size()) {
            res.add(s2[j++]);
        } else if (j == s2.size()) {
            res.add(s1[i++]);
        } else {
            res.add((s1[i].weight < s2[j].weight ? s1[i++] : s2[j++]));
        }
    }
    return res;
}

Vector<DataPoint> combine(const Vector<Vector<DataPoint>>& sequences) {
    if (sequences.size() == 0) {
        return {};
    } else if (sequences.size() == 1) {
        return sequences[0];
    } else if (sequences.size() == 2) {
        return combineTwoSequences(sequences[0], sequences[1]);
    } else {
        int k = sequences.size();
        Vector<Vector<DataPoint>> sequencesLeft, sequencesRight;
        for (int i = 0; i < k; ++i) {
            if (i < k / 2) {
                sequencesLeft.add(sequences[i]);
            } else {
                sequencesRight.add(sequences[i]);
            }
        }
        Vector<DataPoint> left = combine(sequencesLeft);
        Vector<DataPoint> right = combine(sequencesRight);
        return combineTwoSequences(left, right);
    }
}

效果

数组合并的时间复杂度验证